來源:網(wǎng)絡(luò)資源 2022-12-17 13:58:04
復(fù)習
復(fù)習是個好習慣,在進行本篇內(nèi)容之前我們先回憶上一篇內(nèi)容得出的結(jié)論:(還指望我粘貼復(fù)制嗎,當然要你背啦)
復(fù)習完畢,開始正題
1.解析式的由來
上一篇的內(nèi)容,幫我們建立了幾何觀念上的函數(shù)即:函數(shù)是線。只有幾何觀念,對于函數(shù)來講是完全不夠的,屬于缺胳膊少腿,不完整。數(shù)學數(shù)學,沒有代數(shù)就沒有靈魂,所以今天我們來把它的靈魂給它裝進去。畢竟是要裝靈魂嘛,是個技術(shù)活,那就先拿最簡單的練練手,也就是一次函數(shù),看看它的軀殼
噫,花里胡哨,亂七八糟。先拿一個出來,用放大鏡看一下
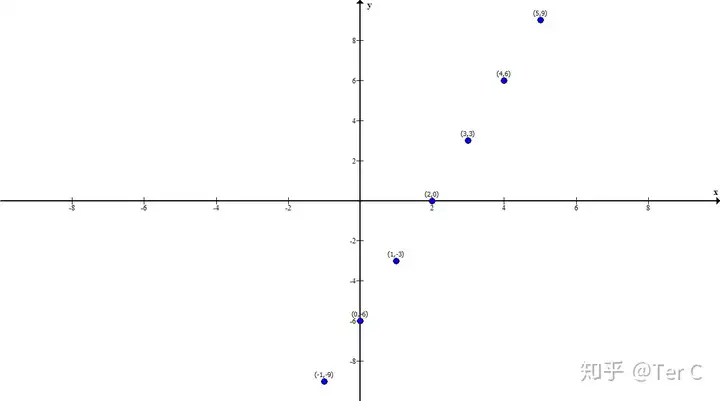
嗯,有那么點兒意思了,原來函數(shù)線真的是由坐標點組成的,我們上一篇的理論就被實錘了。這點被實錘了,那是不是就可以這樣理解函數(shù)的代數(shù)化=坐標點的代數(shù)化。而且,非常巧的是,每一個坐標點都有著相對應(yīng)的橫坐標和縱坐標來表達其身份地位,橫坐標、縱坐標又剛好是數(shù)字。蘋果都砸到你頭上了,下一步該怎么辦不用我多說了吧,當然是把它們列出來好好觀察啊。
(5,9)(4,6)(3,3)(2,0)(1,-3)(0,-6)(-1,-9)
觀察完畢后,按照牛頓的做法,你是不是就想問:為什么這些點在一條直線上?然后我就想一粉筆頭砸你頭上,忘了前一篇的內(nèi)容了?因為它們有規(guī)律啊!!!既然是規(guī)律,那就是變化,是變化按照我們的通用解法,先來個后面的減前面的。這里是坐標點,所以我們就后面的橫坐標減前面的橫坐標,縱坐標同理。
先來橫坐標
4-5=-1
3-4=-1
2-3=-1
1-2=-1
可知都等于-1
再來縱坐標
6-9=-3
3-6=-3
0-3=-3
-3-0=-3
可知都等于-3
看出道道了嘛,反正我看出來了,那就是在相鄰坐標點之間,橫坐標減1,縱坐標要減3,反過來橫坐標加1,縱坐標要加3。這到底對不對呢,不妨做一下驗證,按照這個思路,分別找出(5,9)前面的坐標點和(-1,-9)后面的坐標點。(5,9)前面坐標點的橫坐標為6,從5到6橫坐標加1,那縱坐標加3即點(6,9)同理可得(-1,-9)后面的坐標點為(-2,-12),描點連線
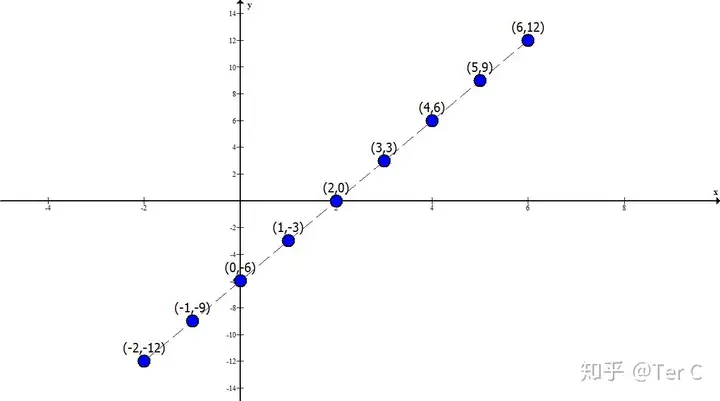
很明顯,新得出的點和原來的點是在一條直線上,證明我們得到的規(guī)律是沒有錯的。既然相鄰坐標點之間,有著橫坐標減1,縱坐標要減3,反過來橫坐標加1,縱坐標要加3這樣的規(guī)律,是不是就萬事大吉了呢?顯然不是,比如,請你找出(-2,-12)之后的第50個坐標點。那你豈不是要重復(fù)上面的做法50遍?50遍你說你行,好,那請問第2020個呢?你還說你行,我再問第20102949203個呢?不行了吧。too young too simple。這就說明我們得到的規(guī)律不夠普遍,不足以用于計算,需要繼續(xù)推廣化。

我們在小學二年級學過加減法的推廣運算是乘除法,我們就把規(guī)律總結(jié)為乘除的規(guī)律即縱坐標的增加量是橫坐標增加量的3倍。先驗證一下符不符合原來的比如(5,9)和(2,0)用一下新得到的規(guī)律
從5到2增加了-3,縱坐標就要增加-9,9+(-9)=0,bingo正確。
后的第50個坐標點再計算(-2,-12)之后的第50個坐標點
在-2后面,又是第50個,所以橫坐標=-52,根據(jù)規(guī)律有縱坐標=-12-50*3=-162
同理可計算任意坐標點
觀察計算過程可知,計算本條直線的任意坐標點,需要用到我們的規(guī)律和一個已知坐標點。
滿足于本條直線坐標點的規(guī)律找到了,別忘了我們的最終目標:規(guī)律代數(shù)化。我們?nèi)我饨o出本條直線上一坐標點(x,y),選取(5,9)為基準坐標點。
縱坐標的增加量
y-9
橫坐標的增加量
x-5
縱坐標的增加量是橫坐標增加量的3倍
y-9=3*(x-5)
得y=3x-6
所以y=3x-6代表了本條線的所有坐標點,進而代表了本條直線
還沒完,這條線是3倍,那有沒有4倍,5倍,6倍,肯定是有的,所以我們就令k=任意常數(shù),順理成章的就把這個規(guī)律推廣到了所有一次函數(shù)線即在一次函數(shù)線中,縱坐標的增加量是橫坐標增加量的k倍。現(xiàn)在要完成這條規(guī)律代數(shù)化,以表達所有的一次函數(shù)線。已知一條一次函數(shù)線,縱坐標的增加量是橫坐標增加量的k倍,已知坐標點(m,n),求任意坐標點(x,y)。
縱坐標的增加量
y-n
橫坐標的增加量
x-m
縱坐標的增加量是橫坐標增加量的k倍
y-n=k*(x-m)
y=kx+n-km(看起來太復(fù)雜不清爽)
不妨令b=n-km
所以y=kx+b
大功告成y=kx+b就是所有一次函數(shù)線的代表
做了這么多的工作,終于把一次函數(shù)從直線變成了y=kx+b這樣一條代數(shù)式,又是求解又是分析的,給這條代數(shù)式起個名字吧就叫解析式。幾何方面的一次函數(shù)都有定義,代數(shù)方面的自然不能少,結(jié)合以上內(nèi)容就是一次函數(shù)的定義形如y=kx+b(k,b為常數(shù),k≠0),其中x為自變量y為因變量,叫做一次函數(shù)
老規(guī)矩總結(jié)一下

perfect,接下來看性質(zhì)

2.相關(guān)性質(zhì)
說到性質(zhì),必然就是考察的重點,也就是痛點了,怎么才能把性質(zhì)記好?喂,這是數(shù)學欸,當然是要理解記憶最好了啊。那我要理解誰呢?喂,解析式都給你了,你看啊,y=kx+b,當然是理解k和b怎么影響函數(shù)了啊
k值怎么影響函數(shù)
從定義里我們知道k=任意常數(shù),我們在小學二年級學過數(shù)是有大小有正負的,就從這兩個方面來看k值對于一次函數(shù)線的影響。
(1)正負
在研究k值,根據(jù)控制變量法,需保持b值不變,干脆一點直接讓b=0。列幾個k值正負不同的解析式,然后作圖觀察
y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x
作圖流程:求點坐標、描點、連線
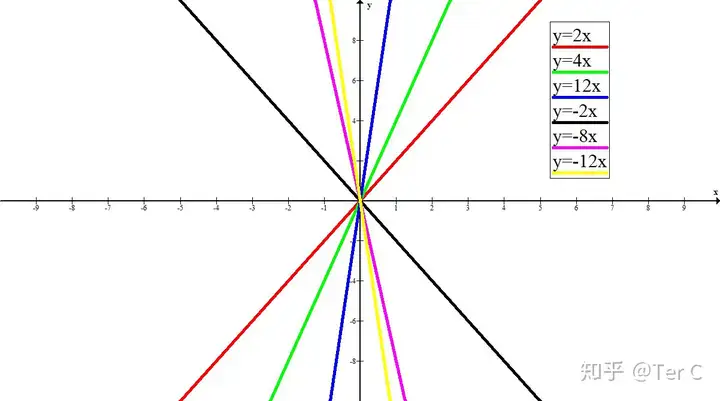
看圖很容易發(fā)現(xiàn)
k>0的一次函數(shù),圖像都經(jīng)過第一、第三象限
k<0的一次函數(shù),圖像都經(jīng)過第二、第四象限
由此可知k值的正負影響著一次函數(shù)坐標點的分布
k的正負不同y隨x的變化情況也不同
(2)大小
研究方法同上,還是它們幾個
y=2x | y=4x | y=12x | y=-2x | y=-8x | y=-12x
作圖流程:求點坐標、描點、連線

可以看到紅、綠、藍三條線的k值分別為2、4、12,很容易發(fā)現(xiàn)
當k>0時
k值越大,圖像與x軸夾角就越大
圖像與x軸夾角永遠都是銳角
當k<0時
k值越大,圖像與x軸夾角也是越大
圖像與x軸夾角永遠都是鈍角
因此k值有個額外稱呼叫:斜率
b值怎么影響函數(shù)
跟k值的研究方法意義,但是我們不能讓k=0,因為定義不允許,因此我們保持k值不變。列幾個k值相同b值不同的大家觀察一下就好了。
y=2x+1 | y=2x+3 | y=2x+5 | y=2x-1 | y=2x-3 | y=2x-5
作圖
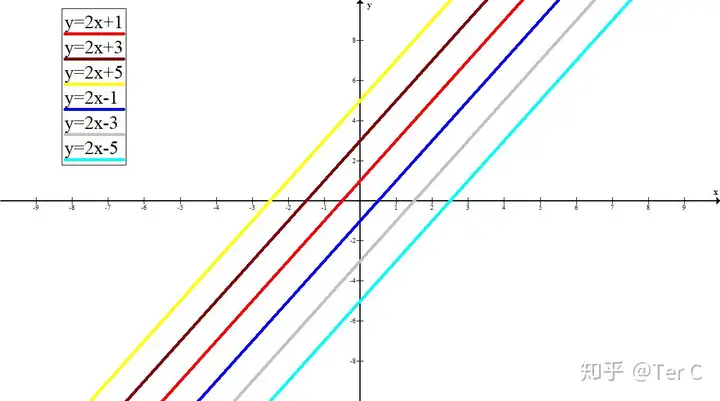
也非常明顯
b>0時
圖像與y軸交于y軸正半軸
b值越大,與y軸交點越靠上
b<0時
圖像與y軸交于y軸負半軸
b值越小,與y軸交點越靠下
還可以發(fā)現(xiàn)
k值相同,直線都是平行的
這些直線都可以用y=2x向上或向下平移相應(yīng)個單位得到
b值也有個額外稱呼叫:截距
小段總結(jié)
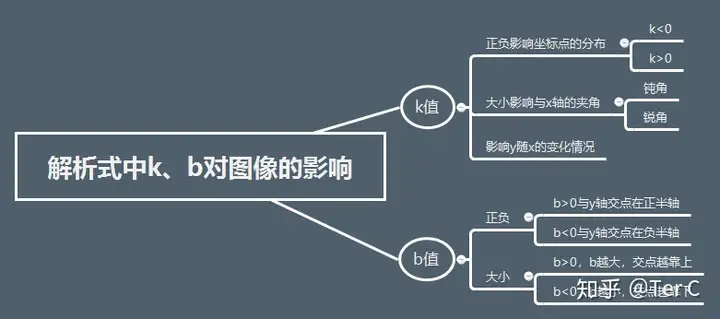
3.相關(guān)考點
(1)圖像考察
#1給圖像辨別k值、b值正負與大小(經(jīng)常與其它函數(shù)結(jié)合)
#2給b值、k值辨別圖像
#3圖像實際應(yīng)用(k>0,第一象限內(nèi))
原理:x值相同,k值越大,y值越大
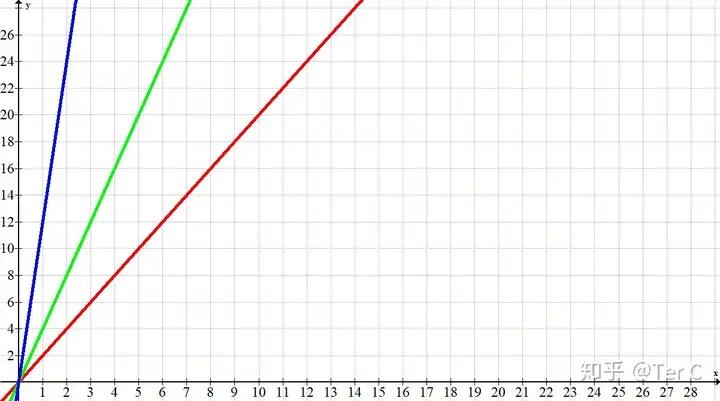
#4如圖所示,當x=5時,y值大小依次是:紅線<綠線<藍線
##考察方式為,把橫縱坐標U/I即為初三物理電學圖像考察,換成m/v即為初二物理質(zhì)量與密度圖像考察,換成F/V即為初二浮力圖像考察,同理還有v-t圖、s-t圖等等,貫穿初高中物理,高中物理還可以用圖像解決復(fù)雜勻加勻減的位移問題
#5化學也同理可換
#6學數(shù)學的同時,把這么多的理化問題都學了,我就問你愛了沒有。真是撿到寶了呢,哈哈哈哈哈
(2)求解析式
#1這個題目的原理就是兩點確定一條直線
知道任意兩點坐標,代入y=kx+b,可得關(guān)于k、b的二元一次方程,解出k、b就可以了,不多說。不會就去學一下二年級學過的解二元一次方程
#2你也可以先求k,再用我教你的計算方法,不過還是推薦課本的解法,還能練習一下解二元一次方程
(3)解應(yīng)用題
#1關(guān)鍵在于設(shè)未知數(shù),列方程,復(fù)雜一點的可能要結(jié)合圖像,考察“數(shù)形結(jié)合”這個數(shù)學思想
#2動點問題里如果關(guān)系式為一次函數(shù)關(guān)系,要結(jié)合取值范圍來求解
(4)與其它函數(shù)組成綜合問題
#1求面積
#2求長度
#3求相應(yīng)的最大最小值,要結(jié)合取值范圍來看
#4求坐標點
(5)函數(shù)與方程
#1只需要理解一點,當y=0時,一次函數(shù)就變成了kx+b=0,也就變成了一元一次方程。
#2從代數(shù)層面看坐標點(x,0)的橫坐標是對應(yīng)方程的解
#3從幾何層面看一次函數(shù)圖像與x軸交點為一個方程點,理解好這里對于二次函數(shù)根的理解很有幫助
(6)函數(shù)與不等式
#1這里還是“數(shù)形結(jié)合”思想的應(yīng)用
#2比如2x+1>0,可以看出y=2x+1這個函數(shù)的y>0,也就是x軸上方的圖像
#3如2x+1>-3x+4,可以看成y1=2x+1與y2=-3x+4這兩個函數(shù)圖像的比較
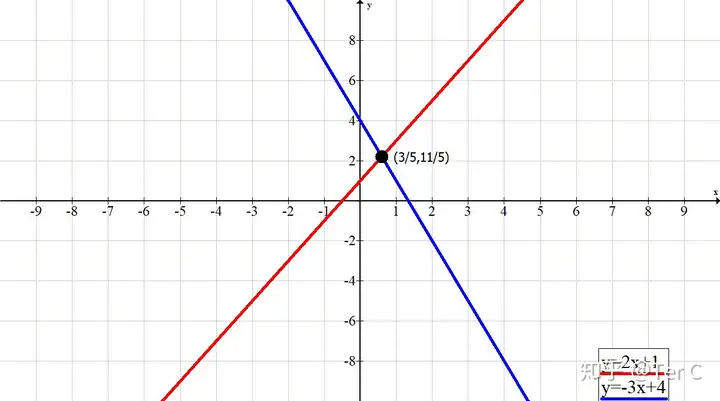
##第一步要找到交點,看圖可知交點坐標為(3/5,11/5)
##沒有交點就是沒有解
##第二步要分兩部分看,交點左邊和交點右邊
##該圖可知交點左邊,藍線騎在紅線頭上,所以是2x+1<-3x+4對應(yīng)不等式的解為x<3/5
##交點右邊是紅線騎在藍線頭上,所以是2x+1>-3x+4對應(yīng)不等式的解為x>3/5
歡迎使用手機、平板等移動設(shè)備訪問中考網(wǎng),2025中考一路陪伴同行!>>點擊查看